概述

在互联网通讯中,加密主要被分为对称加密和非对称加密,其中非对称加密用来建立连接,对称加密用来传输大量数据.

对称密钥加密

对称密钥加密(Symmetric-key algorithm)又称为对称加密 私钥加密 共享密钥加密,是密码学中的一类加密算法.这类算法在加密和解密时使用相同的密钥,或是使用两个可以简单地相互推算的密钥.事实上,这组密钥称为在两个或多个成员间的共同秘密,以便维持专属的通信联系.与公开密钥加密相比,要求双方获取相同的密钥也是对称密钥加密的主要缺点之一.

常见的对称加密算法有DES 3DES AES Blowfish IDEA RC5 RC6.

对称加密的速度比公钥加密快很多,在很多场合都需要对称加密.

非对称加密

公开密钥加密(Public-key cryptography),也称非对称加密(asymmetric cryptography),是密码学的一种算法,它需要两个密钥,一个实公开密钥,另一个是私有密钥;一个用作加密的时候,一个则用作解密.

使用其中一个密钥把明文加密后所得的密文,只能用相对应的另一个密钥才能解密得到原来的明文;甚至连最初用来加密的密钥也不能用作解密.由于加密和解密需要两个不同的密钥,故被称为非对称加密;不同于加密和解密都使用同一个密钥的对称加密.

虽然两个密钥在数学上相关,但如果知道了其中一个,并不能凭此计算出另外一个;因此其中一个可以公开,称为公钥,任意向外发布;不公开的密钥为私钥,必须由用户自行严格秘密保管,决不能通过任何途径向任何人提供,也不会透漏给要通信的另一方,即使他被信任.

基于公开密钥加密的特性,它还提供数字签名的功能,使电子文件可以得到如同在纸本文件上亲笔签署的效果.

加密过程

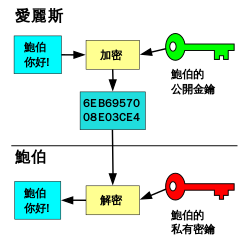
鲍勃将自己的公钥发送到网上,爱丽丝将自己的明文加密后发送到网上,鲍勃使用私钥解密.

除了爱丽丝和鲍勃,没有其它人可以读取到明文.

数字签名

如果一个用户使用他的私钥加密明文,任何人都可以用该用户的公钥解密密文;由于私钥只由该用户持有,故可以肯定该文件必定出自于该用户;公众可以验证该用户发布的数据或文件是否完整 中途是否曾被篡改,接收者可信赖这条信息确实来自于该用户,该用户亦无法抵赖,这被称作数字签名,大部分国家已经立法承认数字签名拥有等同传统亲笔签名的法律效力.

公钥可以通过数字证书认证机构签授的电子证书形式公布,接收者通过信任链形成一套完整的公开密钥基础建设.

例如,从网上下载的安装程序,一般都带有程序制作者的数字签名,可以证明该程序的确是该作者(公司)发布的而不是第三方伪造的且未被篡改过(身份认证/验证).而在网络银行或购物网站,一般也会使用HTTPS,让客户确认他们不是连接到伪冒网站.

与对称密码学的比较

对称密钥加密牵扯到密钥管理的问题,尤其是密钥交换,它需要作者和读者在通信之前先通过另一个安全的渠道交换共用的密钥,才可以安全的把密文通过不安全的渠道发送;对称密钥一旦被窃,其所作的加密将即时失效;而在互联网,如果通信双方分隔异地而素未谋面,则对称加密事先所需要的”安全渠道”变得不可行;非对称加密则容许加密密钥随便发布,解密的私钥不发往任何用户,只在单方保管;如此,即使公钥在网上被截获,如果没有与其匹配的私钥,也无法将诶米,极为适合在互联网上使用.

另一方面,公钥解密的特性可以形成数字签名,使数据和文件受到保护并可信赖;如果公钥通过数字证书认证机构签授成为电子证书,更可作为数字身份的认证,这都是对称密钥加密无法实现的.

不过,公钥加密在计算上相当复杂,性能欠佳 远远不比对称加密;因此,在一般实际情况下,往往通过公钥加密来随机创建临时的对称密钥,亦即对话键,然后才通过对称加密来传输大量 主题的数据.

常见的公钥加密算法有:RSA ELGamal 背包算法 Rabin(RSA的特例) 迪菲－赫尔曼密钥交换协议中的公钥加密算法、椭圆曲线加密算法（英语：Elliptic Curve Cryptography, ECC）.使用最广泛的是RSA算法.

国密算法

国密算法是国密密码局认定的国产密码算法.主要有SM1,SM2,SM3,SM4,密钥长度和分组长度均为128位.

SM1为对称加密.其加密强度与AES相当.该算法不公开,调用该算法时,需要通过加密芯片的接口进行调用.

SM2为非对称加密,基于ECC.该算法已公开.由于该算法基于ECC,故其签名速度与密钥生成速度都快于RSA.ECC 256位(SM2采用的就是ECC256位的一种)安全强度比RSA2048位高,但运算速度快于RSA.

SM3消息摘要.可以用MD5作为对比理解.该算法已公开.校验结果为256位.

SM4无线局域网标准的分组数据算法.对称加密,密钥长度和分组长度均为128位.